紹介
高校では数学でいろいろ勉強したと思います。私は、エンジニアだったので習った数学は仕事でバンバン使いましたが、多くの社会人は、あれっていったい何だったの?と思っていると思います。今、高校で勉強している人も、何に役立つの?と思っていると思います。その代表格にサイン、コサイン、タンジェントという三角関数があると思います。現に私の高校時代でも、サイン、コサイン、何になる、人生の本質に関係ないじゃない、と言う友達はいました。
私は通信系のエンジニアでしたので、三角関数は仕事に役立ちました。それを応用して世の中に役にたつ製品を出してきたと思います。またそれで生活をしてきました。
でも、高校時代、三角関数を習得するのには、苦労したことは確かです。
ここから始まる記事は、メーカに勤めた事があり、数学を実際に使ったことのある冴子先生が、三角関数をイメージ的にわかりやすく説明してくれます。これを機会に、皆さんには、三角関数をもっと身近に感じてもらったり、あるいは、非常に興味を持ち、エンジニアになり、実際に使ってもらえるようになれば幸いです。
第1話 サインとは

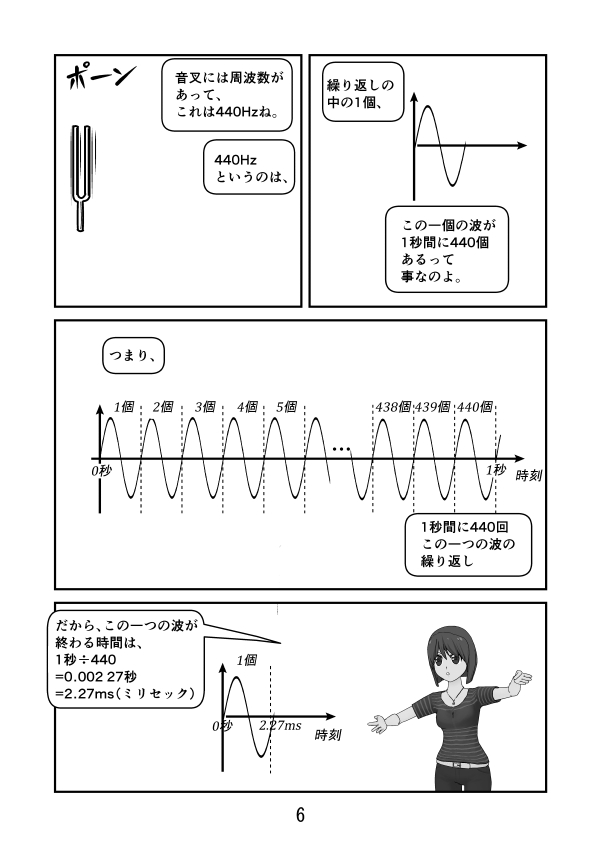
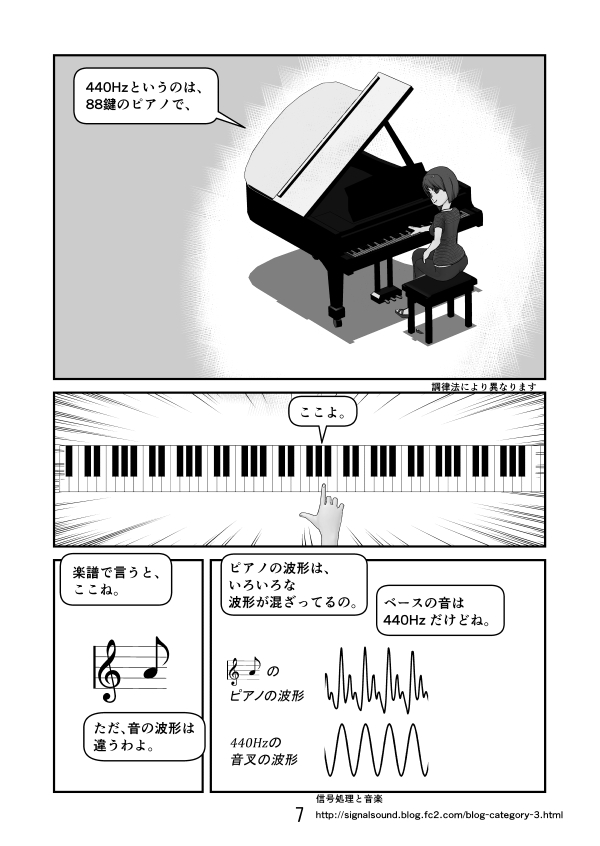
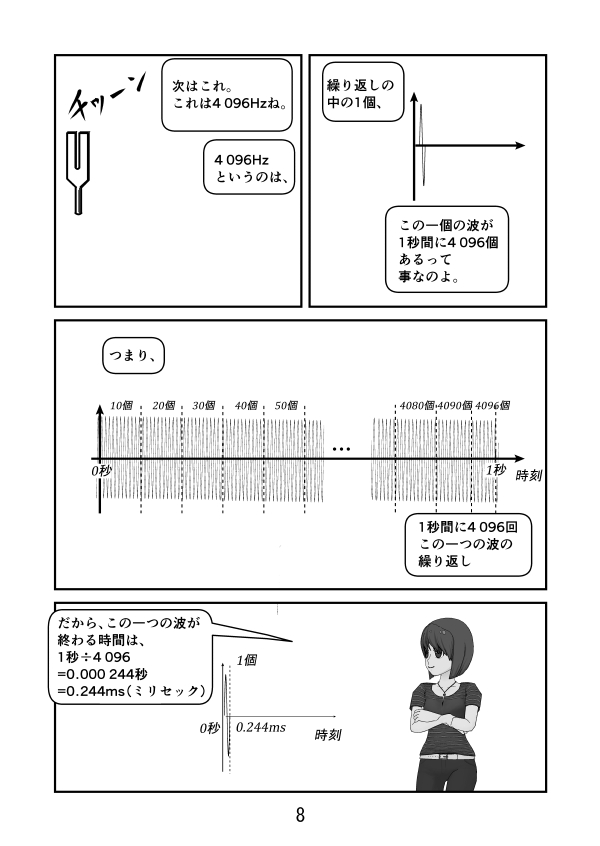


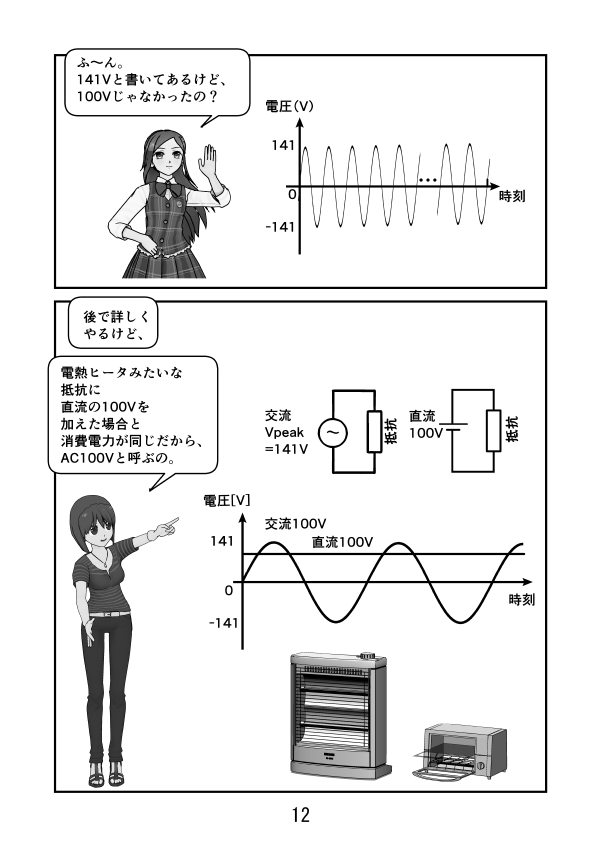
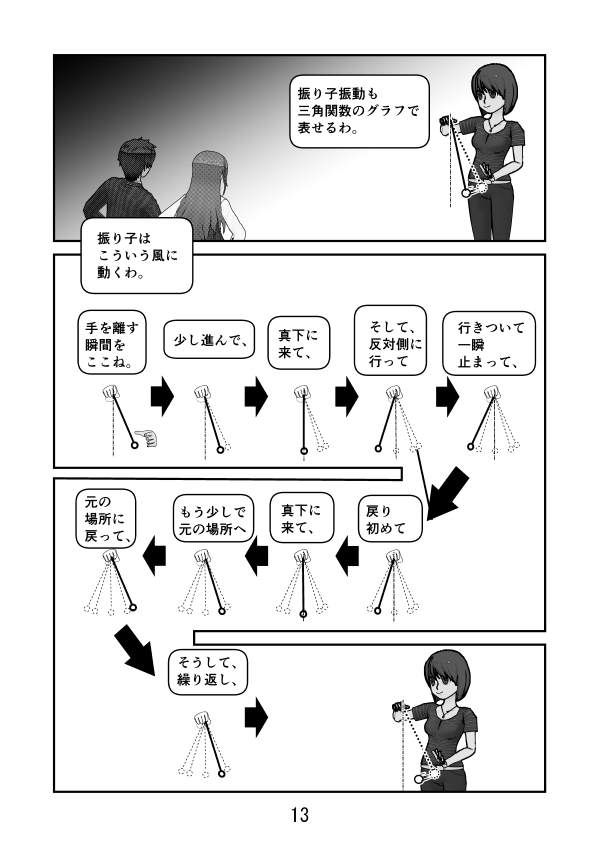
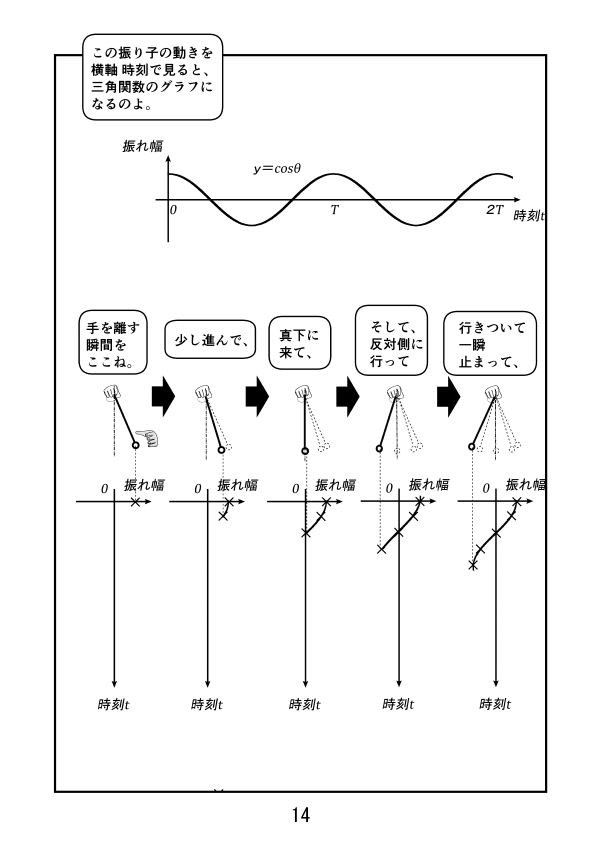
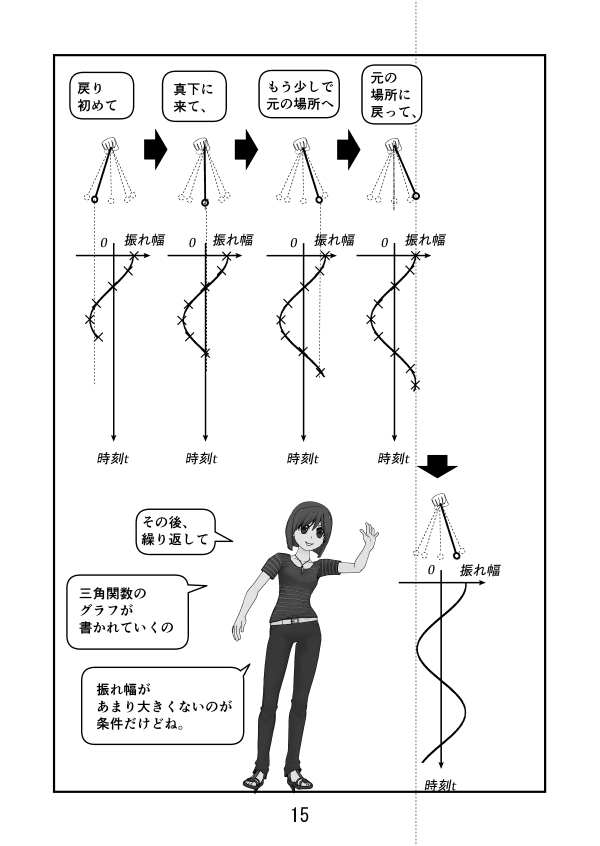


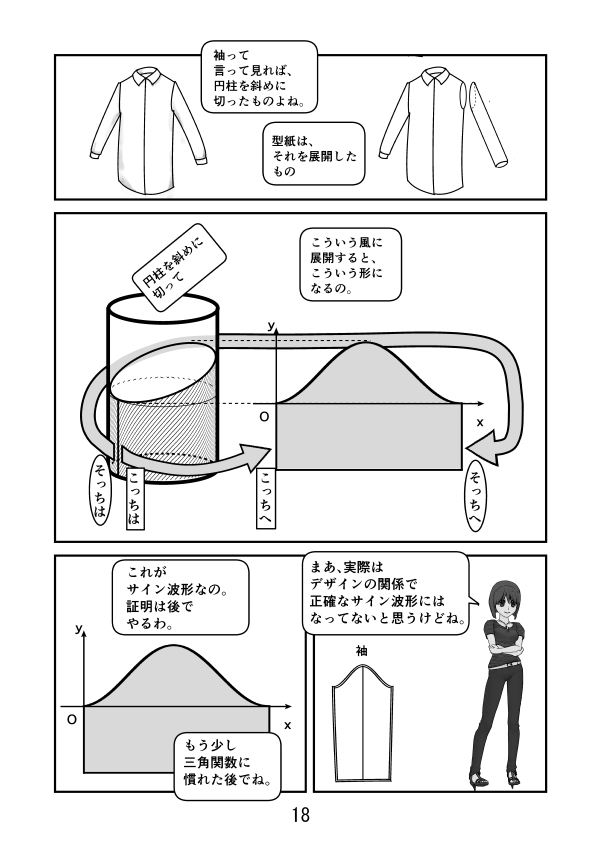

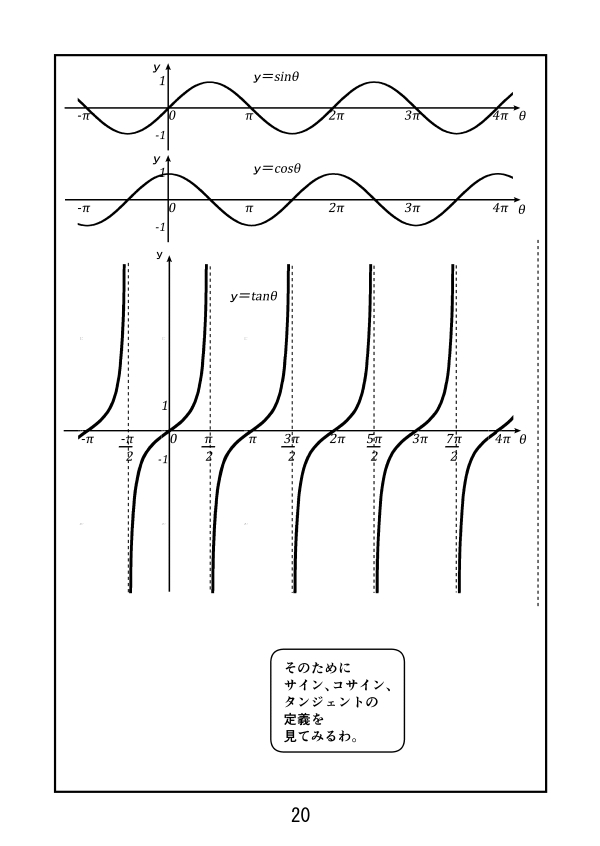
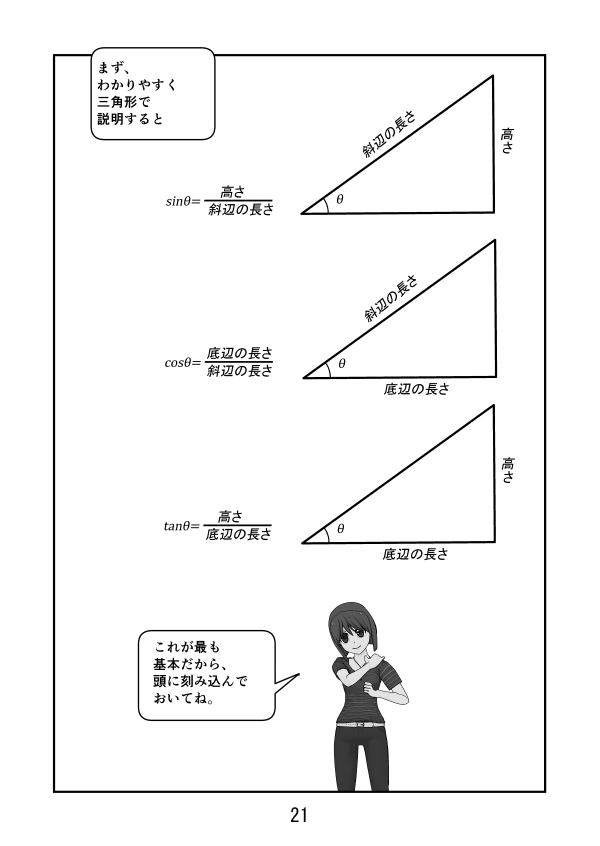
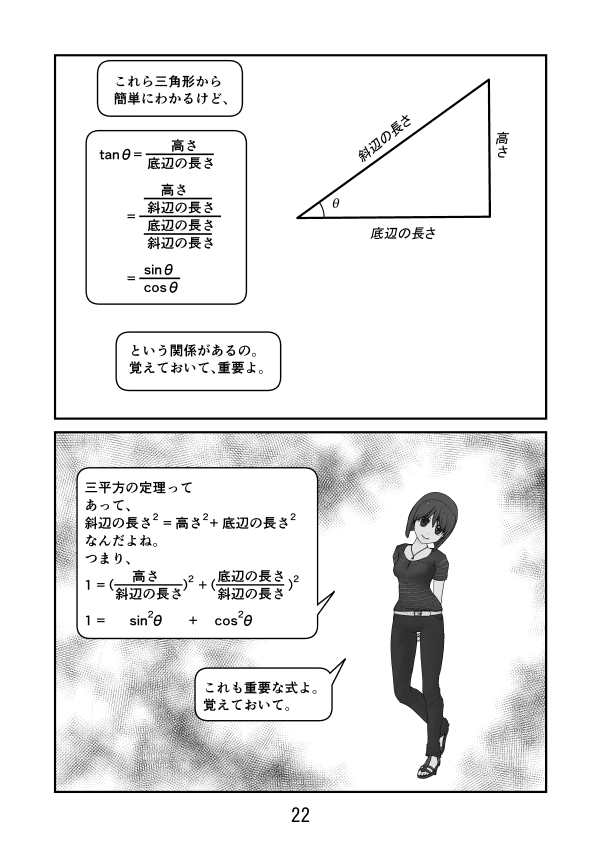

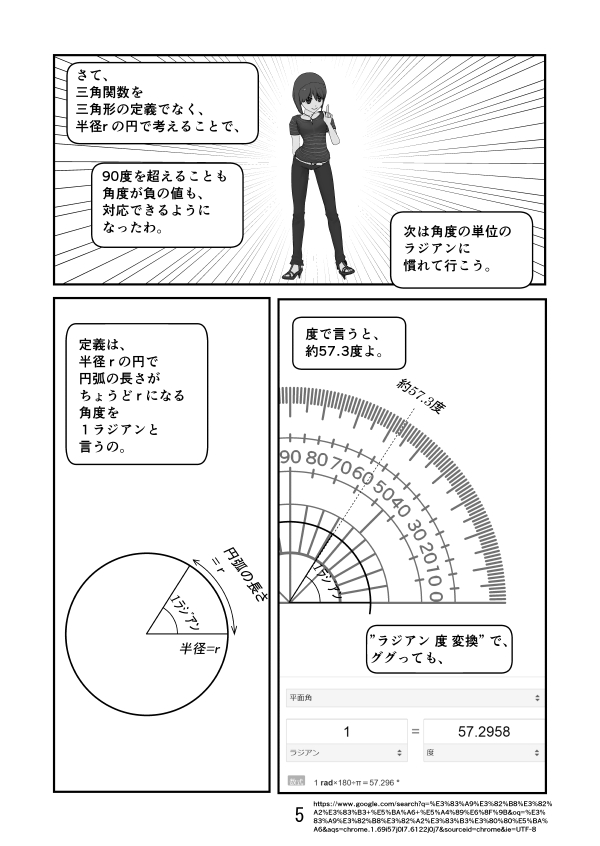
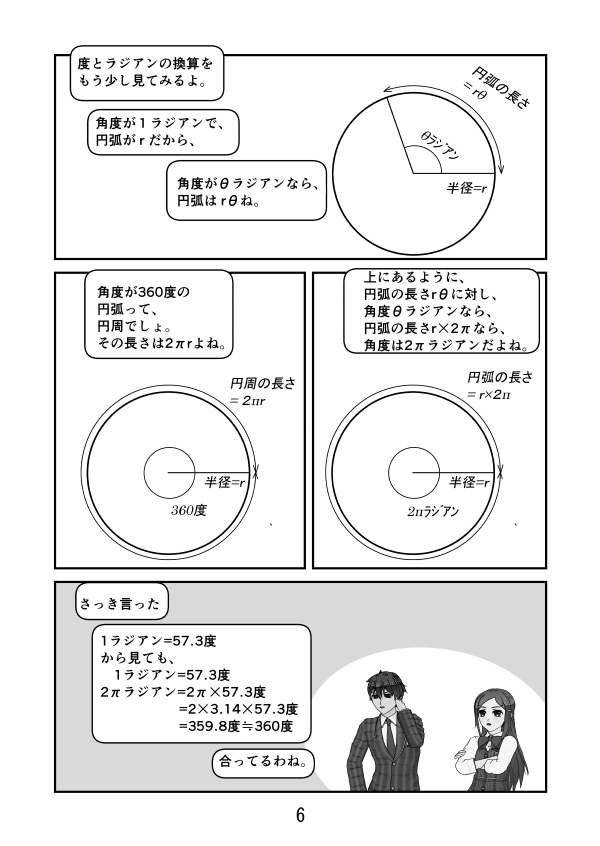
第2話 ラジアンとは
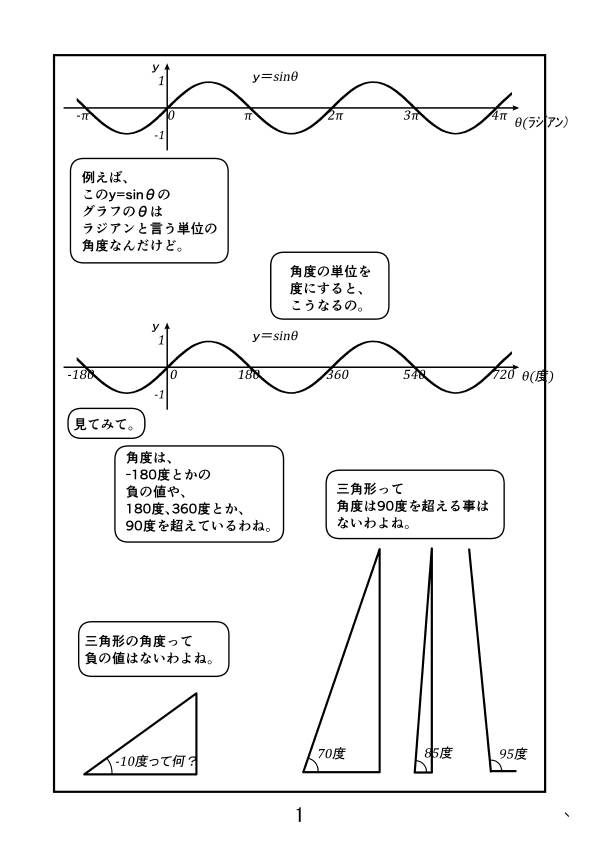
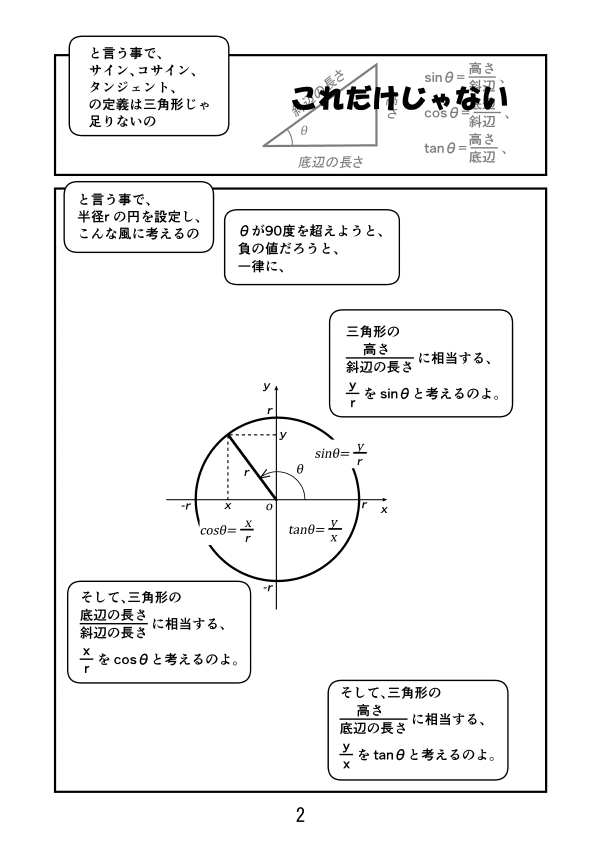
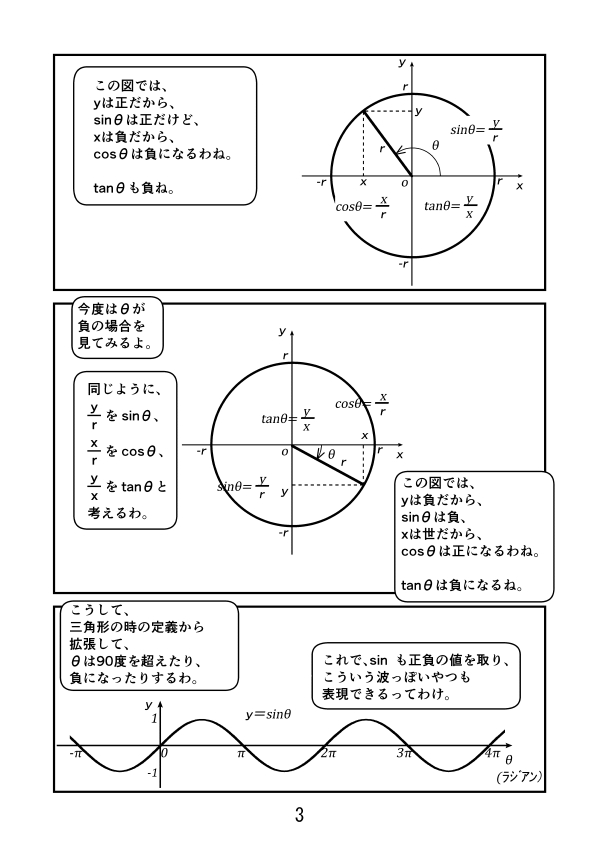
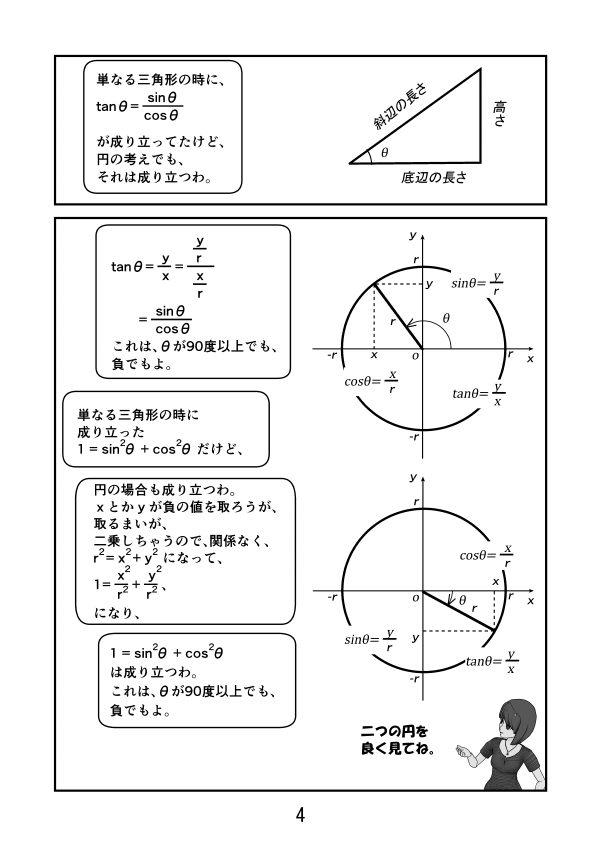
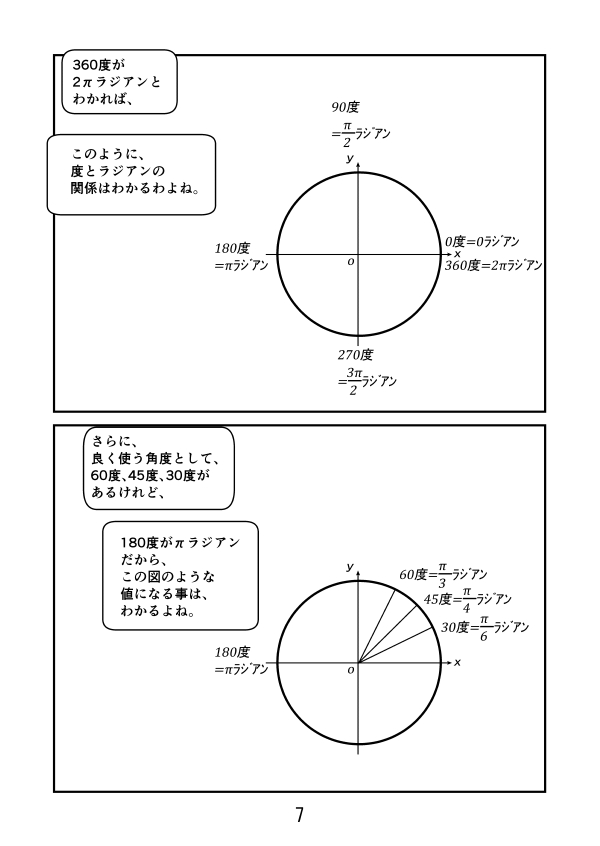
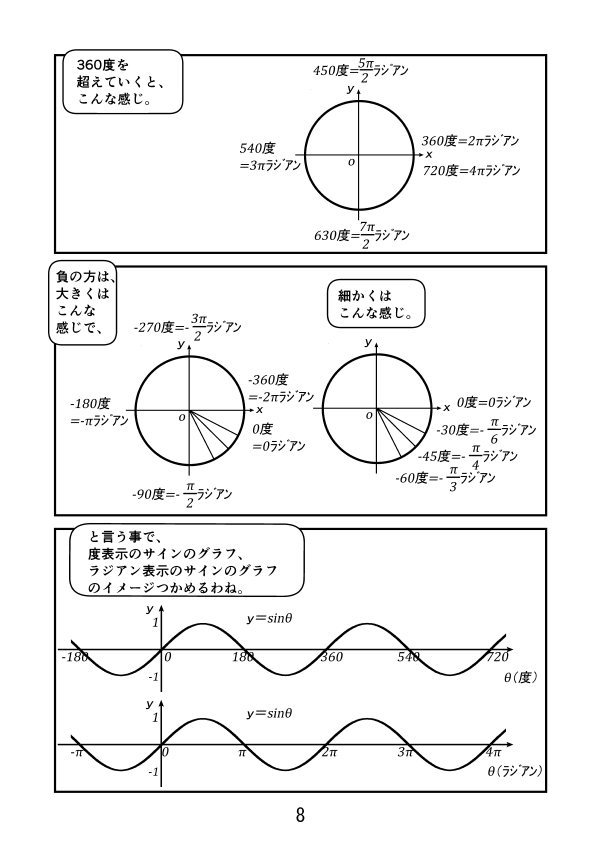
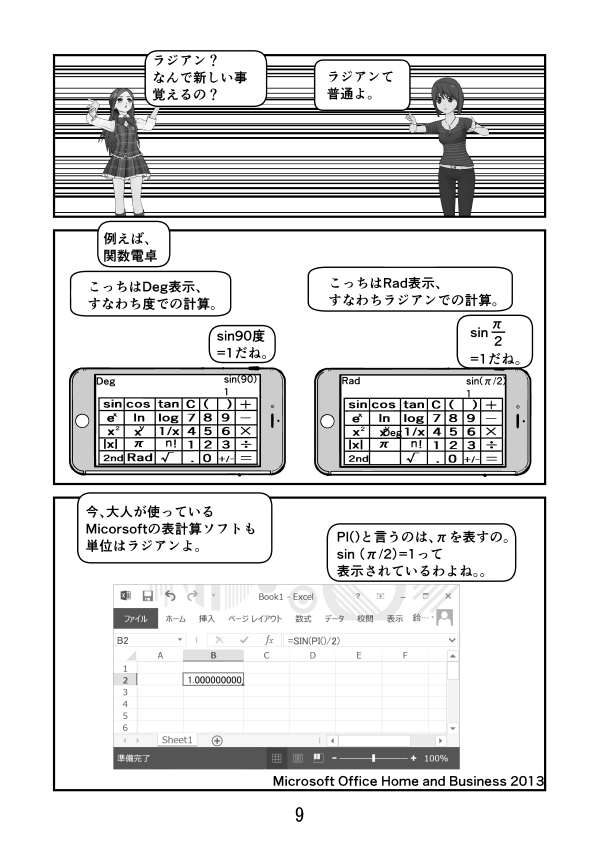

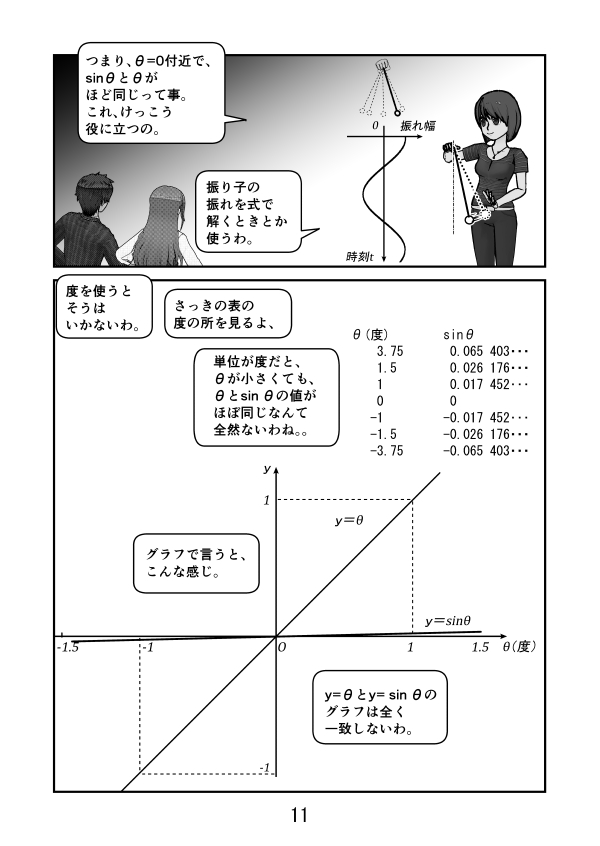
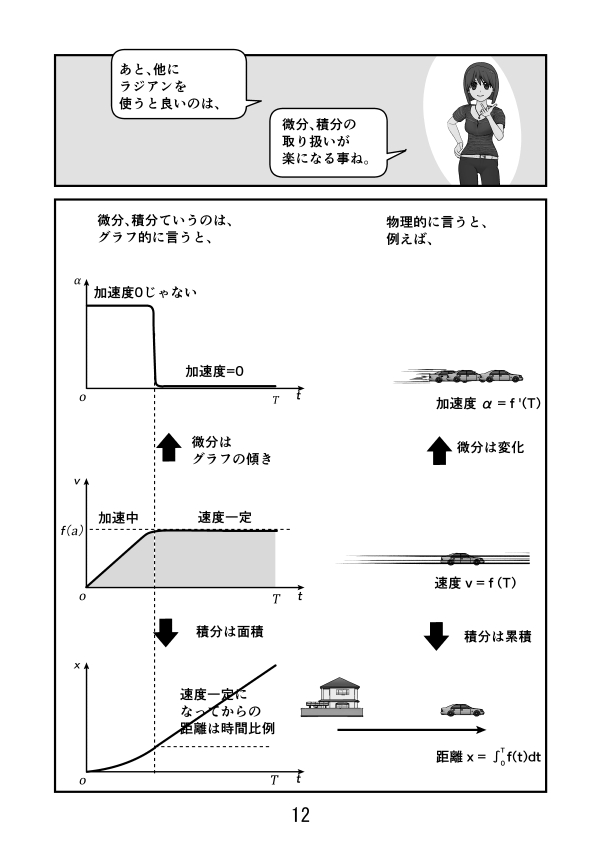
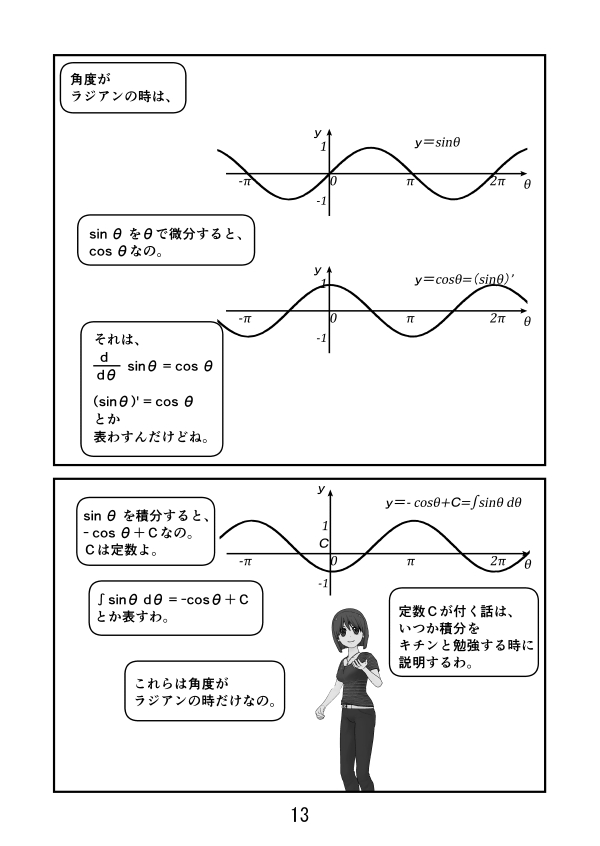
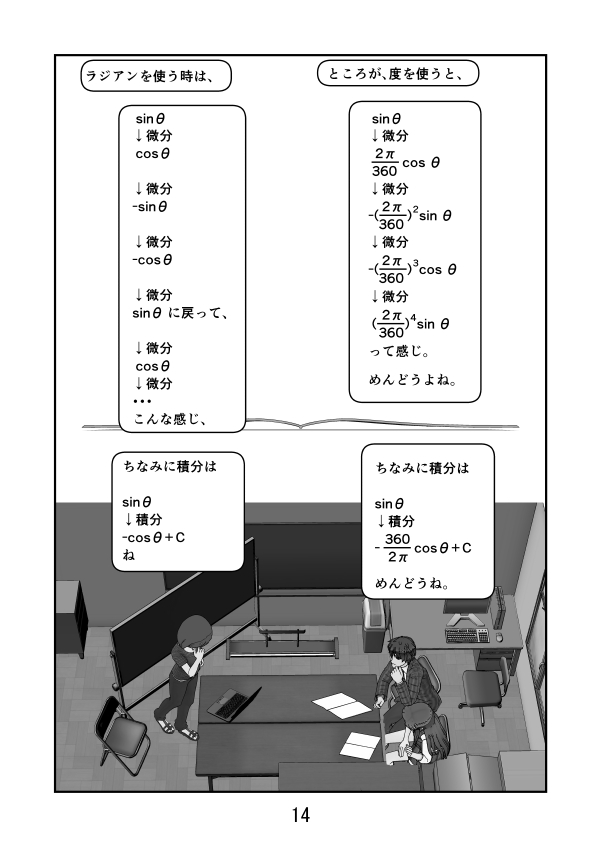
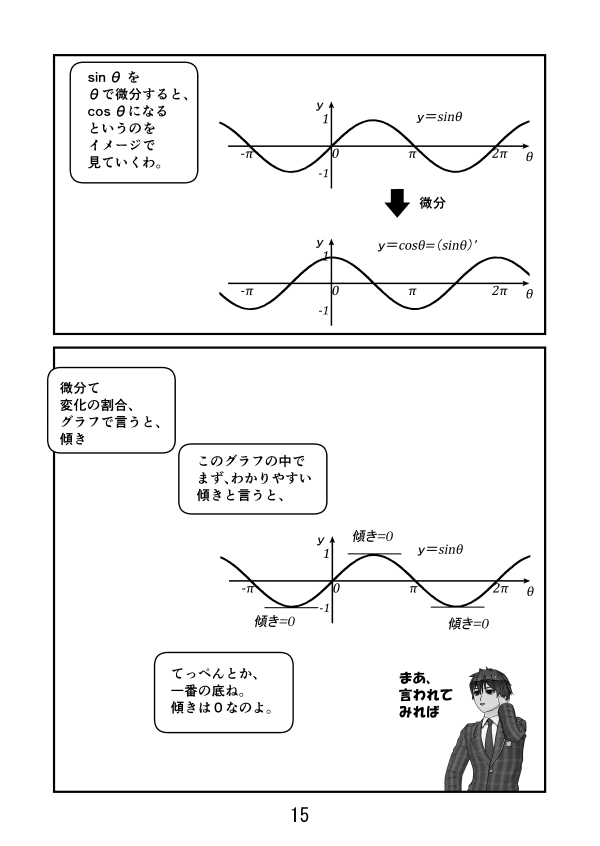
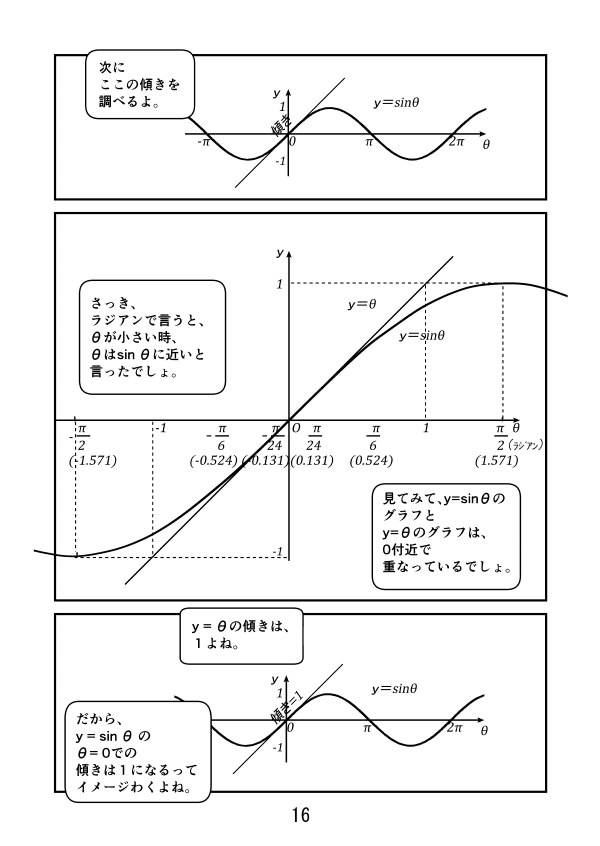
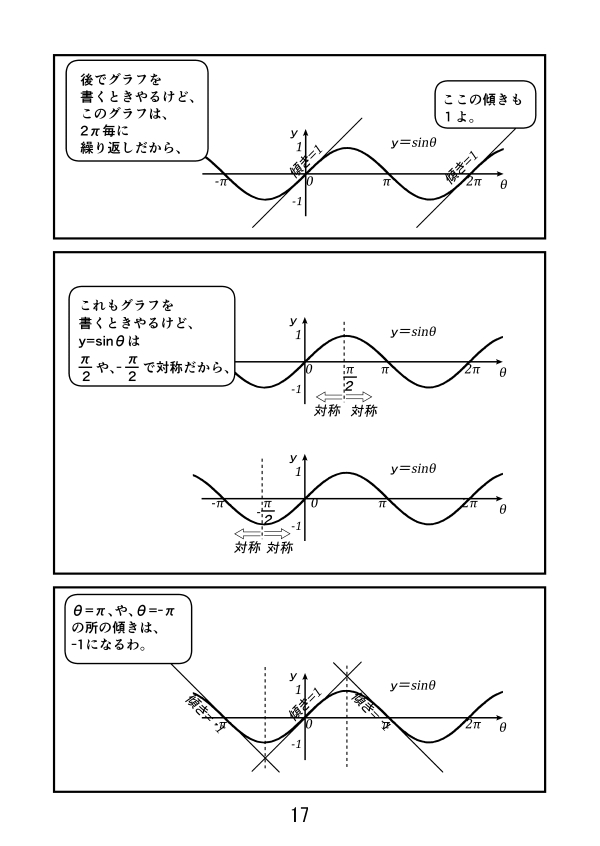
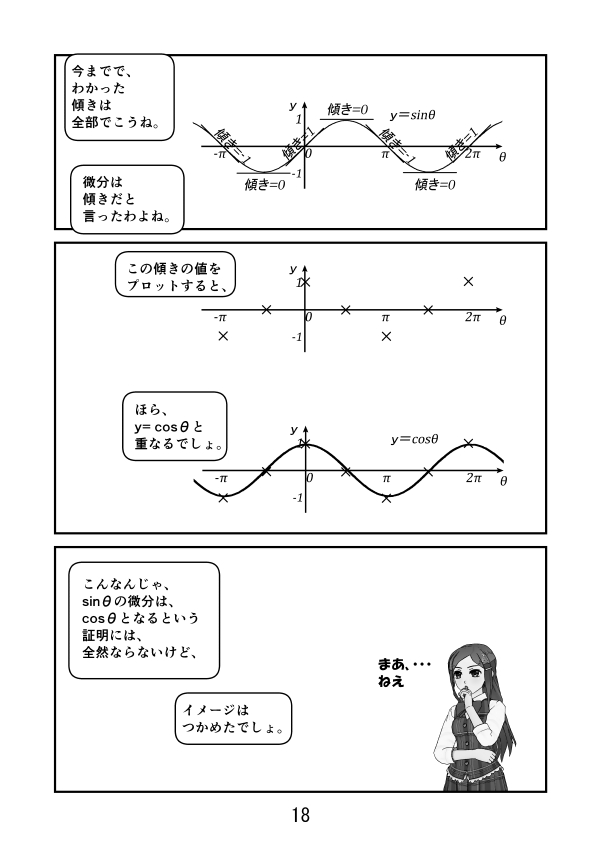


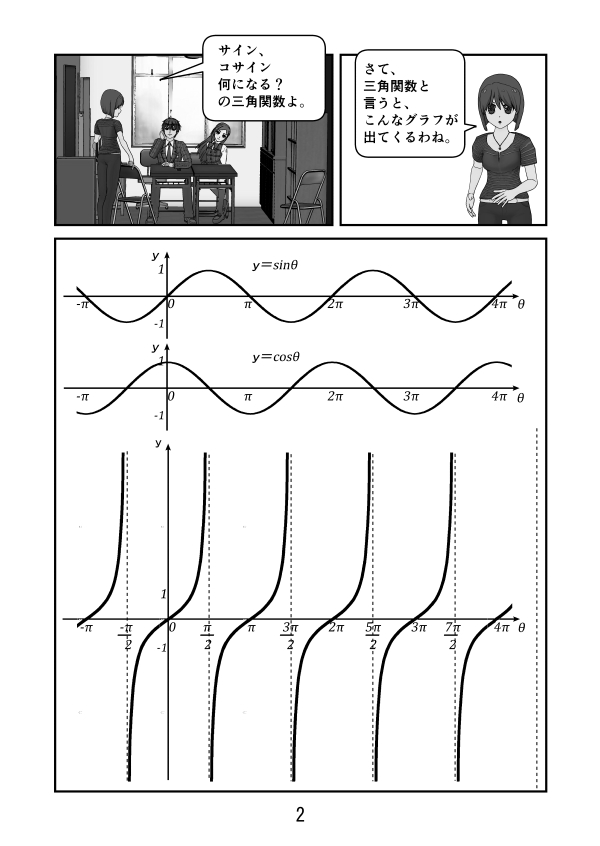
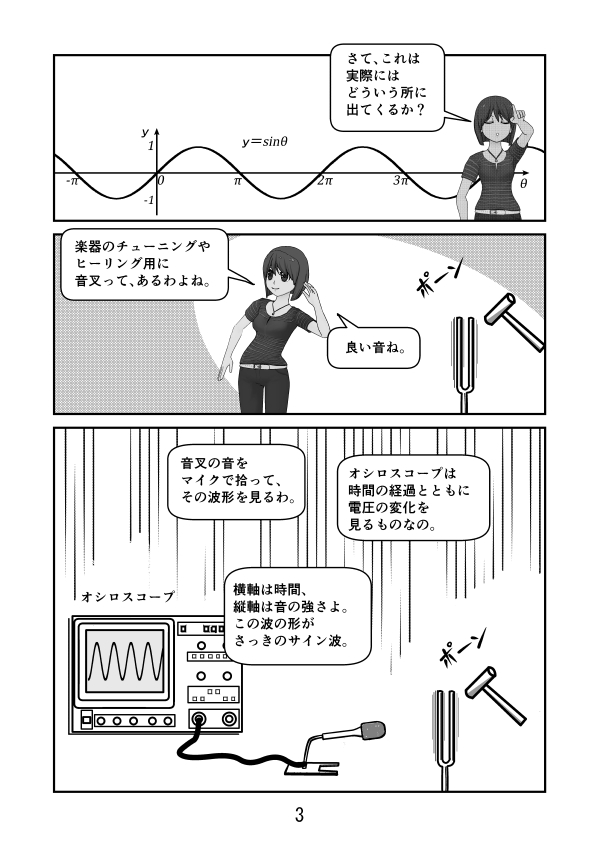
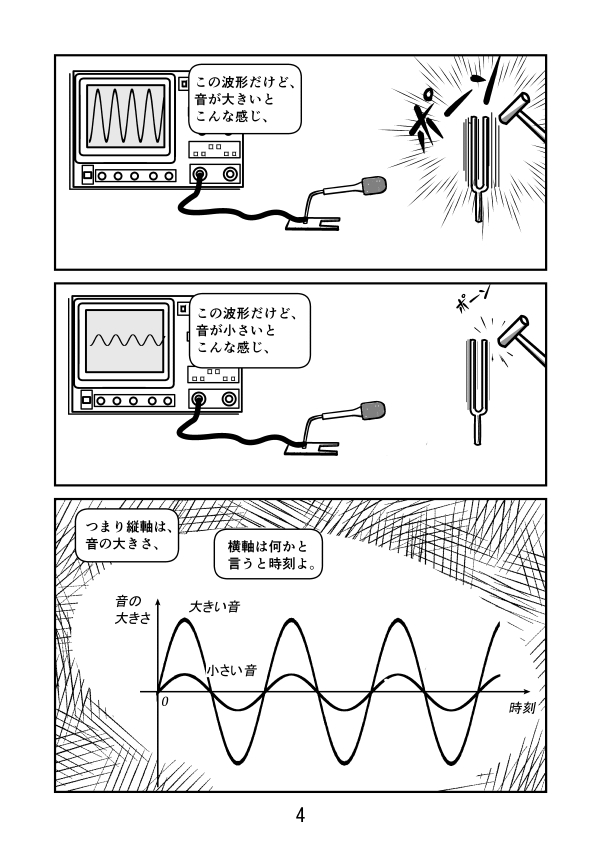
第3話 サイン、コサイン、タンジェントのグラフ




























第4話 三角関数のグラフの性質










































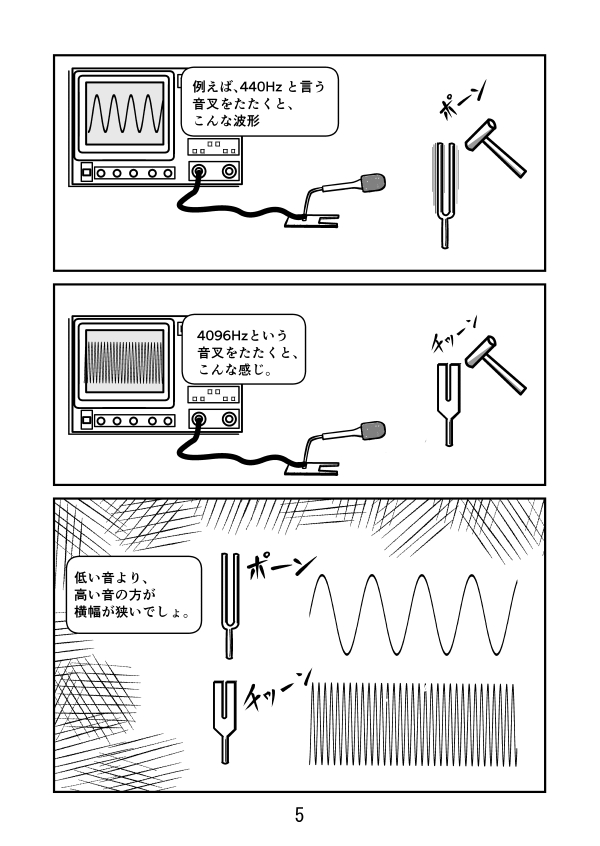
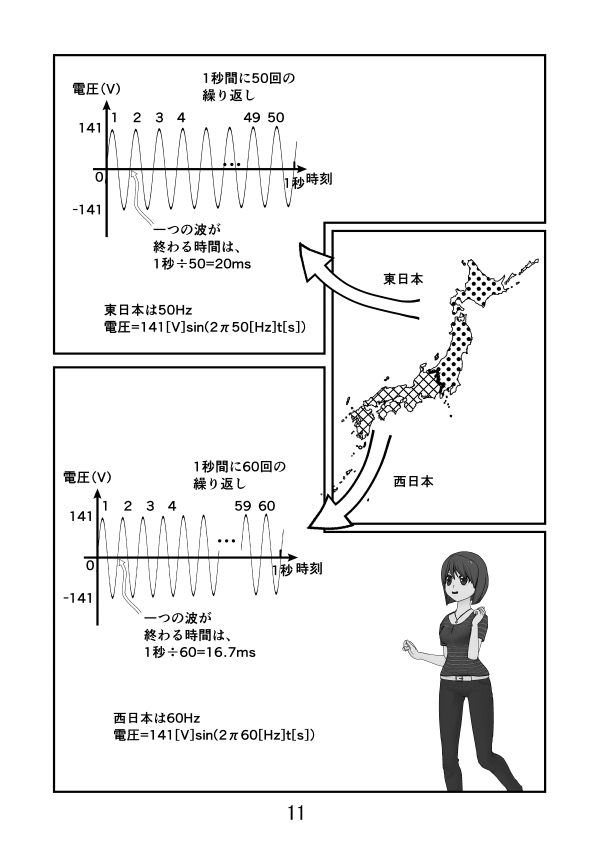
![50Hzと言うのは、1周期T[s]=1[秒]÷50 = 20[ms]。時間T[s]で1周するというのは、y=sin 2π/T[s]×t[s]で表される。](https://manabi100.com/wp-content/uploads/2021/01/イメージでわかる冴子先生の高校数学_043.jpg)
![y=sin2π/T[s]×t[s]、東日本ではT[s] = 20[ms]、西日本ではT[s] = 16.7[ms]](https://manabi100.com/wp-content/uploads/2020/12/イメージでわかる冴子先生の高校数学_044.jpg)


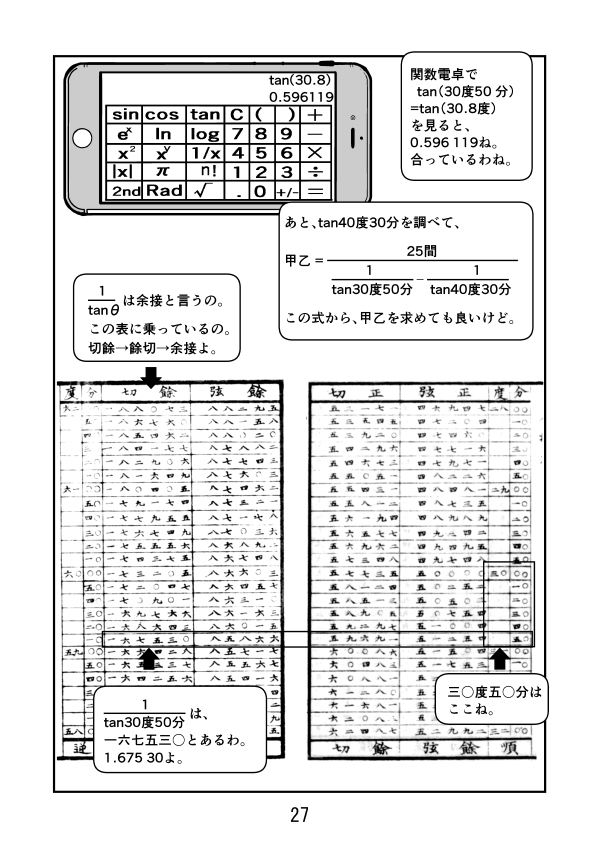
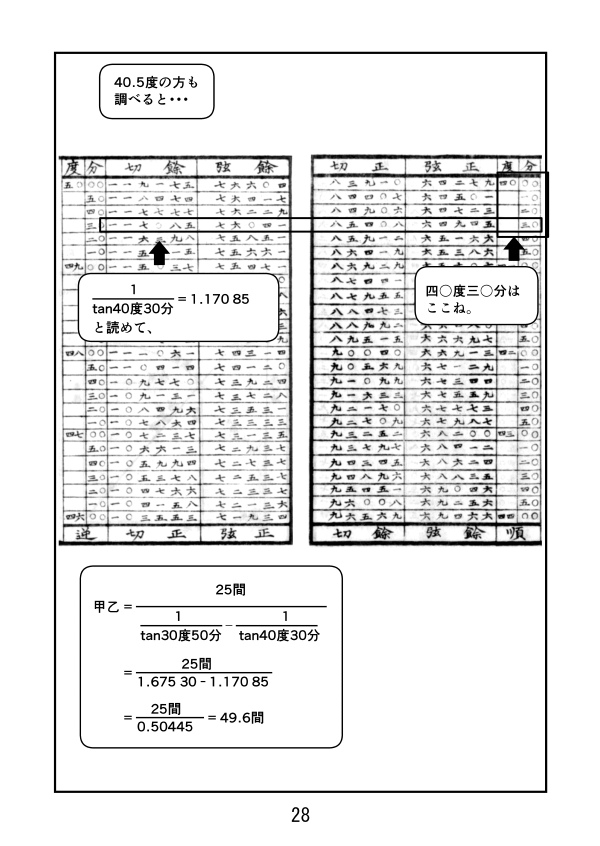
第5話 値を求める




























































第6話 応用編







