漫画で高校数学 y=sinθをθで微分するとcosθになるのをイメージ的に見てましょう2 三角関数17
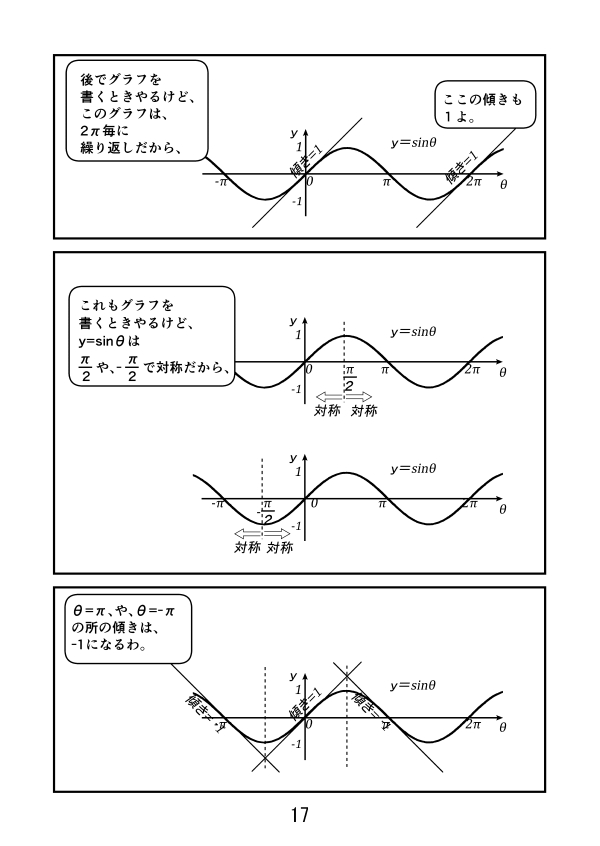
y=sinθ のグラフで、θ=0 の時の傾きは1。グラフは2$π$毎に繰り返しだから、θ=2$π$のところの傾きも1になります。
y=sinθ のグラフは、θ=$\frac{π}{2}$や -$\frac{π}{2}$ で対称だから、θ=$π$や-$π$での傾きは-1になります。
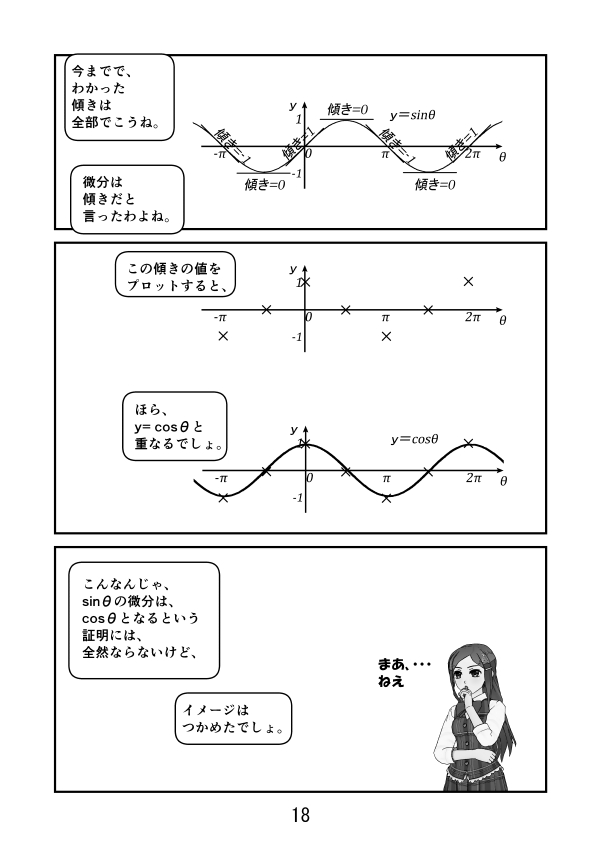
そうすると、y=sinθ のグラフは、θ=-$π$、-$\frac{π}{2}$、0、$\frac{π}{2}$、$π$、$\frac{3π}{2}$、2$π$で、傾きはそれぞれ-1、0、1、0、-1、0、1。
これをプロットすると、y=cosθ のグラフと重なります。
これでは、y=sinθ を微分すると、y=cosθ になることの証明には全然なってませんが、イメージはつかめると思います。